حل مسئله N Queen
مسئله نَسَخَ نَسخَ (N Queen) یکی از مسائل کلاسیک در علم کامپیوتر و ریاضیات است. هدف این مسئله قرار دادن N ملکه بر روی یک صفحه شطرنج N در N به گونهای است که هیچ دو ملکهای یکدیگر را تهدید نکنند. به عبارتی دیگر، هیچ دو ملکه نباید در یک ردیف، یک ستون یا یک قطر قرار گیرند.
چالشها و راهحلها
این مسئله از نظر نظری و عملی چالشبرانگیز است. با افزایش تعداد ملکهها، تعداد راهحلها بهطور تصاعدی افزایش مییابد. برای مثال، برای 8 ملکه، 92 راهحل مختلف وجود دارد.
استراتژیهای مختلفی برای حل این مسئله وجود دارد، از جمله:
- روش بازگشتی (Backtracking): این روش یکی از متداولترین رویکردها برای حل مسئله N Queen است. در این روش، ملکهها یکی یکی بر روی صفحه قرار میگیرند. اگر در هر مرحله، قرار دادن ملکه به گونهای باشد که تهدیدی برای دیگر ملکهها ایجاد نکند، سپس به مرحله بعدی میرود. اگر در نهایت هیچ راهحلی وجود نداشته باشد، به عقب برمیگردد و ملکه را در موقعیت دیگری قرار میدهد.
- روشهای جستجوی عمیق (Depth-First Search): این روش به جستجوی عمیق در فضای حل مسئله میپردازد. با استفاده از این تکنیک، میتوان به طور کارآمدی به بررسی تمامی ترکیبهای ممکن پرداخت.
- روشهای الگوریتم ژنتیک: با استفاده از الگوریتمهای تکاملی، میتوان به بهینهسازی و پیدا کردن راهحلهای مناسب برای مسئله N Queen پرداخت. این روشها با شبیهسازی طبیعت و فرایند انتخاب طبیعی کار میکنند.
پیادهسازی
برای پیادهسازی این الگوریتمها، میتوان از زبانهای برنامهنویسی مختلفی استفاده کرد. در اینجا یک مثال ساده از پیادهسازی الگوریتم بازگشتی در زبان پایتون آورده شده است:
```python
def is_safe(board, row, col):
# بررسی ردیفها و ستونها
for i in range(col):
if board[row][i] == 1:
return False
# بررسی diagonals
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
for i, j in zip(range(row, len(board)), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solve_n_queen_util(board, col):
if col >= len(board):
return True
for i in range(len(board)):
if is_safe(board, i, col):
board[i][col] = 1
if solve_n_queen_util(board, col + 1):
return True
board[i][col] = 0
return False
def solve_n_queen(n):
board = [[0 for _ in range(n)] for _ in range(n)]
if not solve_n_queen_util(board, 0):
return False
print_board(board)
def print_board(board):
for row in board:
print(" ".join("Q" if cell else "." for cell in row))
solve_n_queen(8)
```
نتیجهگیری
مسئله N Queen به عنوان یک چالش جذاب در الگوریتمها و برنامهنویسی، نه تنها به ما کمک میکند تا تکنیکهای مختلفی را به کار ببریم بلکه باعث بهبود تفکر منطقی و مهارتهای حل مسئله ما نیز میشود. این مسئله، پایهگذار بسیاری از الگوریتمهای پیشرفته و تکنیکهای جستجو در علم کامپیوتر است.
حل مسئلهی N وزیرحل مسئلهی N وزیر با نمایشحل مسئلهی N وزیر در سی شارپحل مسئله هشت وزیرحل مسئله N-Queen در سی شارپحل مساله n وزیرحل مسله 9 وزیر در سی شارپn وزیر در سی شارپحل مسئله N QueenN Queen سی شارپالگوریتم DFS N Queenالگوریتم BFS N Queenبرنامه نویسی سی شارپمسئله N Queen در سی شارپحل مسائل الگوریتمیN Queen با استفاده از DFSN Queen با استفاده از BFSآموزش N Queen سی شارپ
حل مسئله N-Queen با استفاده از DFS و BFS
مسئله N-Queen یکی از چالشهای مشهور در علم کامپیوتر و ریاضیات است. هدف اصلی این است که N ملکه را بر روی یک صفحه شطرنج N در N قرار دهید به طوری که هیچ دو ملکهای یکدیگر را تهدید نکنند.
در این لینک، روشی برای حل این مسئله با استفاده از دو الگوریتم محبوب، یعنی جستجوی عمقاول (DFS) و جستجوی عرضاول (BFS) ارائه شده است.
جستجوی عمقاول (DFS)
در DFS، ابتدا به یک شاخه از درخت جستجو میرویم و تا جایی که ممکن است ادامه میدهیم. این روش برای مسائل ترکیبی مانند N-Queen بسیار کارآمد است. در اینجا، برای هر موقعیت ملکه، بررسی میکنیم که آیا میتوانیم آن را در مکان مورد نظر قرار دهیم یا خیر. اگر ممکن باشد، به محل بعدی میرویم و این فرآیند را تکرار میکنیم.
جستجوی عرضاول (BFS)
در مقابل، BFS به طور همزمان همهی گزینهها را در یک سطح بررسی میکند. این روش معمولاً برای مسائل کوچکتر بهتر عمل میکند و در اینجا نیز میتواند برای جستجوی تمامی ترکیبها استفاده شود. با گسترش همهی گزینهها در یک سطح، میتوانیم تمام حالتهای ممکن را بررسی کنیم.
نکات مهم
- هر دو روش، بهینهسازیهایی دارند که میتوانند سرعت جستجو را افزایش دهند.
- در نهایت، نتیجهی هر دو الگوریتم میتواند به ما کمک کند تا راهحلهای مختلف را برای مسئله N-Queen پیدا کنیم.
به طور کلی، این لینک یک منبع مفید برای کسانی است که به دنبال درک عمیقتری از حل مسئله N-Queen هستند. با بهرهگیری از این الگوریتمها، میتوانند به راهحلهای کارآمدتری دست یابند.
یک فایل در موضوع (نمونه سورس کد حل مسئله N-Queen توسط DFS و BFS و نمایش آن در سی شارپ) آماده کرده ایم که از لینک زیر می توانید دانلود فرمایید برای دانلود کردن به لینک زیر بروید
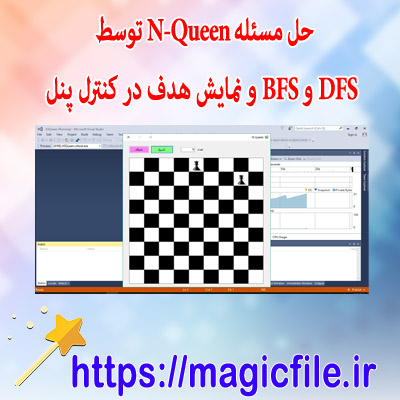
منبع : https://magicfile.ir
- یکشنبه ۰۴ خرداد ۰۴ | ۱۰:۲۱
- ۶ بازديد
- ۰ نظر
 پاورپوینت درباره طبیعت
پاورپوینت درباره طبیعت نرمافزارهای تحلیل دادههای اجتماعی
نرمافزارهای تحلیل دادههای اجتماعی فیلترهای بورس ایران
فیلترهای بورس ایران نرم افزار مقایسه قیمت موبایل
نرم افزار مقایسه قیمت موبایل نقد و بررسی اسکرینپیت
نقد و بررسی اسکرینپیت PHP داروسازی
PHP داروسازی